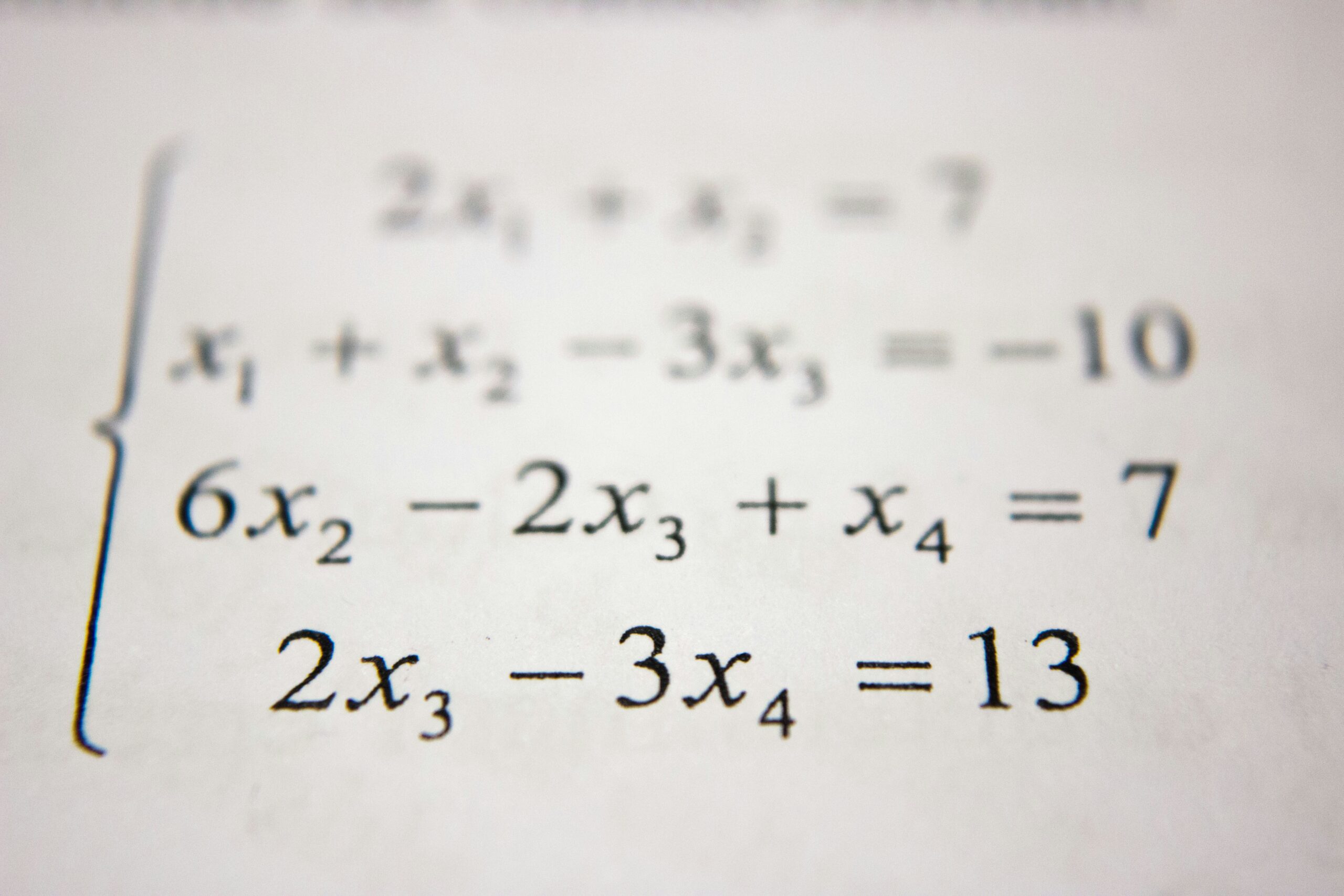数理論理学とは、数学的な命題や証明、論理的推論の構造を形式的に研究する分野です。論理的な体系や公理、証明の技法を探求し、数学やコンピュータサイエンスなどでの論理的な基盤を提供します。数理論理学は、数学の理論的な基盤を固め、形式的な証明や論理的な推論の正確性を保証します。
数理論理学を学ぶメリットは、論理的思考力や証明能力を向上させることです。形式的な論理体系や証明技法を理解することで、数学的な問題解決やコンピュータサイエンスの基礎が強化されます。また、抽象的な思考力が養われ、複雑な問題に対するアプローチが洗練されます。
はじめての数理論理学
論理学に初めて触れる人のために、やさしい言葉で数理論理学の基礎を解説しています。命題論理や述語論理を中心に、丁寧な図解と例題が理解を助けます。
数理論理学 (現代基礎数学)
論理式の構造から証明論、完全性定理までを体系的に学べる一冊です。大学初級から中級レベルに対応しており、数学の厳密な論理に触れることができます。
復刊 数理論理学序説
古典的な教科書として定評のある入門書で、形式体系とその理論的背景をわかりやすく紹介しています。初学者にも親しみやすく、今なお根強い人気を誇ります。
復刊 現代数理論理学入門
形式言語や構文、意味論の基本からモデル理論まで幅広くカバーしています。現代的なアプローチで論理学の全体像をとらえる力を養える内容です。
数理論理学―使い方と考え方:超準解析の入口まで
理論だけでなく、実際にどのように使われるかを重視した構成です。超準解析の入り口まで視野に入れており、応用的な理解にもつながります。
スマリヤン 数理論理学講義 上巻
独特の語り口で論理学の奥深さを伝える名著です。命題論理から述語論理に至るまでの基礎を、ユーモアとともに楽しみながら学べる構成となっています。
スマリヤン数理論理学講義 下巻
上巻に続き、完全性定理や不完全性定理など高度なテーマを扱います。論理的推論の力を深めたい読者にとって、挑戦しがいのある内容となっています。
まとめ
数理論理学の本を読むことは、単なる数学の学習にとどまりません。それは、物事を正確にとらえ、論理的に整理し、筋道立てて伝える力を養うことに繋がります。普段の生活や仕事の中では、直感や感情に頼ることも多いものですが、数理論理学を通じて「なぜそう考えるのか」を自分の中で明確にできるようになります。
たとえば、ある議論の中で相手の主張が論理的に矛盾していることに気づいたとき、その矛盾を明快に説明できる力があると、対話の質が大きく向上します。これは仕事のプレゼンテーションや問題解決、チームとのコミュニケーションにも役立ちます。また、論理構造に対する理解は、文章の構成や読解力にも良い影響を与えます。
さらに、数理論理学はデジタル社会における「言語」のような存在です。コンピュータが何かを判断する際の仕組みや、プログラムの正しさを証明する方法にも応用されており、今後ますます重要性が高まる分野です。この本で基礎的な概念を身につければ、人工知能やデータ分析といった分野への入り口にもなり得ます。
加えて、数理論理学には思考の「無駄を削ぐ力」があります。複雑な問題を簡潔に整理し、核心に迫る思考法は、時間管理や意思決定の精度を高めてくれます。これは忙しい日常を送る人にとって、大きな武器になるでしょう。
人生において、感情や偶然が重要な役割を果たすのは確かですが、それだけでは対応しきれない局面もあります。そんなとき、論理という「確かな土台」があれば、迷わずに次の一歩を踏み出せます。数理論理学の本は、その土台を築くための道具です。
読者の皆さんがこの本を手に取ることで、思考に深さと精度を加え、理性的に物事を判断できる力を得られることを願っています。論理的な思考は一朝一夕で身につくものではありませんが、一歩ずつ学んでいけば、確実に人生をより豊かで明晰なものにしてくれます。